О «размерности» физических величин
О «размерности» физических величин.
(метрологический аспект).
В. П. Макаров
Российский государственный геологоразведочный университет. Москва.
При анализе с помощью изотопных и геохимических геотермометров баротермических условий формирования минералов используются представления равновесной термодинамики. Однако при этом слабо учитывается специфика геологических исследований: геологические задачи относятся к категории обратных, обладающих высокой степенью неопределенности. Кроме того геологические исследования имеют примитивный и поверхностных характер, что также повышает степень неопределённости их решения. Поэтому уменьшение этой неопределенности способствует повышению надежности геологичских решений. Проведенные исследования [2, 7, 8] выявили недостаточную четкость формулировок основных понятий термодинамики, необходимых для решения обратных задач термодинамики термобарогеохимии). К ним относятся представления об обратимых реакциях, понятия «равновесия», «идеальности– неидеальности» и пр. Следовательно, одним из способов уменьшения этой неопределенности является более строгий подход к формированию понятийной базы. Эта задача решается, в частности, на основе использования представлений теории размерностей, элементы которой отражены в [5]
А. Все множество числовых значений единственным образом делится на непересекающиеся подмножества (классы) этих значений.
I. Класс размерных физических величин. Перед формулированием понятия множества этого класса опишем элемент этого множества. Этот элемент называется «физической величиной» и определяет «свойство в качественном отношении общее многим физическим объектам (физическим системам, их состояниям и происходящим процессам), но в количественном отношении индивидуальное для каждого объекта» [5].
Размер физической величины – это количественное содержание в данном объекте свойства, соответствующего понятию «физическая величина» и отражаемое понятием «единицы измерения». Тогда значение Х физической величины – это оценка физической величины в виде некоторого отвлеченного числа (х) принятых для нее единиц [х]. Число (х), входящее в значение физической величины, называется числовым значением этой величины, а [х] – размерностью этой величины. В свете этого значение Х некоторой физической величины можно выразить через равенство
Х= (х)[х], (1)
причем запись (х)[х]– не перестановочна, т.е. Х≠[х](х). Величина Х называется размерной величиной. Далее запись [Х] будет обозначать размерность физической величины Х.
Отметим некоторые свойства этого произведения:
a. При сложении двух физических величин X=(x)[x] и Y= (y)[y], у которых [x]= [y], общий элемент может выноситься за скобки: (х)[х]+ (y)[y]= (х)[х]+ (y)[x]= ((x)+(y))[x].
б. Если Х=(х)[х], Y=(y)[y], то Х+Y= Y+ X. Действительно, X+Y= (х)[х]+(y)[y]= ((x)+(y))[x]= ((y)+ (x))[x]= (y)[y]+ (x)[x]= Y+ X, то - есть сложение физических величин перестановочно.
Пусть даны элементы А = (a)[a]; B= (b)[b]; C= (c)[c], D = (d)[d]; [a]= [b]= [c] =[d], обладающие свойствами:
1). A+ B= (a)[a]+ (b)[a] = (a)[a]+ (b)[a] = ((a)+ (b)) [a], т. е. [a] можно выносить за пределы скобок (…). Полагая (a)+ (b)= (c), получаем ((a)+ (b))[c]= (c)[c]. Таким образом, A+ B= C.
2). Сумма A + B перестановочна: А + В = (a)[a] + (b)[b] = (a)[a]+ (b)[a]= ((a)+ (b))[a]= ((b)+ (a))[a]= (b)[а] +(а)[а] =(b)[b] +(a)[a]= B + A.
3). Для физических величин А и В, для которых (a) = (b) и [a] = [b], существует разность А - В: А - В= (a)[a]- (b)[b]= ((a) - (b))[a]. Поскольку разность отвлеченных чисел существует, то есть (a)- (b) = (d), то это и доказывает теорему. Если при этом (a) = (b) = (d), то получаем величину D= (d)[d], т. е. А - В= D. Физические величины A и B при условии [a] = [b] равны, если (a)= (b). A-B = (a)[a] - (b)[b]= ((a)-(b))[a]. Если (a) = (b), то следует постулируемый вывод. Такие физические величины будем называть равными физическими величинами.
4). Дана операция R (отношение). Элементы A, B, C принадлежат множеству Ω (далее обозначаемому через [Ω]), если ARB= C, т.е.элемент А находится в некотором отношении R к элементу B и результатом отношения является элемент С.
5). Если R= S (сумма), то [Ω]– множество значений таких физических величин, что среди любых элементов [Ω] можно найти элементы A, B, С и D, для которых A+ B= C и А- В= D. Эти физические величины будем называть однородными, а [Ω]– множеством однородных физических величин. Однородность означает, что не только 1 кг муки и 1 кг меди принадлежат разным множествам [мука] и [Cu], но и 1 кг меди и 1 кг железа принадлежат разным множествам [Cu] и [Fe] соответственно.
6). Множество [Ω] однородных физических величин не содержит операцию арифметического умножения, т.е. R≠П (роизведение), это означает, что отсутствует элемент F= А х В (F = (f)[f]). Действительно, во множестве [Ω] не определено равенство [a][b]= [f]. Это означает, что не определено произведение 1 кг муки на 1 кг меди. Так же физически не определено, что означает произведение 1 кг меди на 1 кг меди. Если же физически возможно создание такого произведения, например, при измерении работы, скорости или др., то эти величины образуют иное множество, отличное от описываемого. В этом случае композиции этих величин присваивается новое обозначение (новый термин), например, работа, энергия, скорость и пр. В связи с этим в [Ω] не определены все операции, вытекающие из операции умножения: возведение в степень, логарифмирование, извлечение корня. Поэтому в [Ω] с элементами A, B и C, физически не определены такие выражения, как lnA, BC и т.д. Действительно, известны, например, значения ln2 или 23, но не выражений ln(2кг) и (2кг) (3кг); то же относится к величинам lnP, lnT и lnV.
II. Класс безразмерных величин. Формально он включает элементы числовой оси, т.е. числа, не имеющие привязки к определенным физическим явлениям. Это не определение, поскольку не ясен механизм получения чисел. Этот класс важен тем, что именно в нем определены все основные арифметические и следуемые из них другие операции (произведение, возведение в степень, логарифмирование, извлечение корней и пр.).
Пусть произвольные элементы A, B, C, D, F из множества [Ω] однородных элементов (т.е. (A, B, C, D, F)⊃ [Ω] (⊃– знак принадлежности)). Тогда для любого элемента A есть такое действительное число N и элемент F, что NA= F.
Сложение равных физических величин может быть заменено умножением этой величины на число N, равное числу этих физических величин. Действительно для двух равных физических величин А и А
F = А+ А= (a)[a]+(a)[a]=((a)+(a))[a]= (2(a))[a]= (2a)[a]= 2А.
Доказательство для большего числа проводится по индукции. Тогда NA= F означает, что F получено сложением величины A последовательно N раз.
Этим введена операция умножения физических величин на некоторое действительное число «N». Для отношений двух величин имеем F/А =(f)[f]/(a)[a]; так как [a] = [f], то они сокращаются. В остатке получается величина F/А = ( f)/(a), не имеющая размерности. Такая величина, обозначаемая через N, называется безразмерной (или безразмерное число), т.е. [N]= 0. Поэтому безразмерное число- это частное от деления друг на друга значений двух однородных физических величин. Для любого безразмерного числа Х будем писать [Х]= 0. Если Х – размерная величина, то будем писать [Х] =1 ≠ 0.
Следствие 1. Поскольку A = (a)[a], F= (f)[f] и [a] = [f], то в дроби F/А допускается сокращение [a] и [f].
Следствие 2. Пусть А= (a)[a] и B= (b)[b] – две однородные величины из множества [Ω], т.е. (А, В) ⊃Ω. Построим отношение А/В: А/В
=((a)[a])/((b)[b])=((a)/(b))х ([a]/[b]). Так как [a]=[b], то А/В= ((a)/(b)) =N.
Если (А, В) É Ω, то для Х= А/(А+ В) [X]= 0. Действительно, отношение Х представим следующим образом: X = А/(А+ В) = ((a)[a])/((a)[a] + ((b)[b]) =((a)[a])/(((a) + (b))[a]) = (a)/((a)+ (b))), откуда следует указанный вывод.
Используется и отношение Y= AM1/(AM1+ BM2), где АМ1⊃ Ω1 и ВМ2 ⊃ Ω2 (результаты химического анализа, выражаемые в %; мольные доли и пр.). Это частично однородные элементы: у них одна размерность, но разная физическая сущность (Сu – мука, Cu – Fe и пр.). Так как не определена сумма АМ1+ ВМ2 , то не ясен смысл Y и выражений типа lnY; понятно, что [lnY] ≠0.
Б. Измеряемую величину M можно представить [5] как произведение M = m[m], где m – число, дающее количественную характеристику параметра, а [m] – выражение, характеризующее наименование единицы измерения этой величины (метры, килограммы и пр.). Например, масса M(Fe) куска железа равна 2 (=m) кг (= [m]), т.е. M(Fe)= 2 кг. Тогда lnM = ln(m[m]) = lnm + ln[m]. Например, ln(2 кг) = ln2 + ln(кг). И если ln2 – величина известная, то смысл величины ln(кг) совершенно не ясен.
Проведенный анализ и примеры с мукой и медью показывают недостаточность существующего определения понятия «размерность». Поэтому для устранения этого недостатка понятие «размерность» дополним новым свойством {X}, характеризующим качество изучаемой величины, т.е. M(X) = m[m]{X}. В приведенном выше примере {X}= Fe. Для величин М1= m1[m1]{X1} и М2= m2[m2]{X2} их отношение N имеет вид:
Если {Х1} = {Х2} и [m1] = [m2], то эти параметры сократятся и получаем N = m1/m2, откуда [N] = [m1/m2] = 0. Если же {Х1}≠ {Х2}, то даже при сокращении [m1] и [m2], [N*] = [N][{Х1}/{Х2}] ≠ 0. То же самое будет, если {Х1} = {Х2}, но [m1] ≠[m2]. Полученное данной процедурой число N по определению называется безразмерной величиной. Число N* не является таковым. Например, число N = (2кгСu)/(5кгСu) –безразмерная величина; но N* = (2кгСu)/(2кг муки), или D* = (2кгСu)/ (2мСu) или D** = (2кгCu)/(2кгFe) величины не безразмерные. В важных случаях выражению [{Х1}/{Х2}] обычно дается новое название [4] (например, г/см3- плотность, м/сек - скорость и пр.).
В термодинамике в бинарной системе (a; b), в котором a и b – содержания некоторых разных химических элементов, отношение a/(a + b) определяет мольную долю вещества в системе. Для величин M(X) = m[m]{X} и N(Y) = n[n]{Y} (обычно [m] = [n]) мольная доля вещества M(X) определится отношением
Для определения размерности отношения проведем преобразования, отраженные в последних двух членах равенства. Поскольку [2] = [n/m] = 0, то размерность величины [M(X)/(M(X)+N(Y))] определяется размерностью отношения [{Y}/{Х}]. Если {Х}≠ {Y}, то [{Y}/{Х}] ≠ 0. Следовательно, [M(X)/[M(X)+N(Y)]]≠ 0. Другими словами, мольные отношения не являются безразмерными величинами, а потому всякие операции типа lnM не имеют физического смысла. Примерами корректных уравнений являются выражения: А= RТ1n(V2/V1) [3, стр.49] (здесь А– работа) или D= Doехр(-Е/RТ), но выражение lnD = lnDo - E/RT уже не является таковым, хотя [E/RT] = 0. В этом выражении не определены величины lnD и lnDo.
Приведем примеры частично однородных величин:
1). Закон Рауля в форме Рi= ХiРo [3, стр.148], Рo и Рi – давление пара над чистым растворителем и раствором, содержащим Xi мольных долей растворенного вещества. Поскольку [Xi] ≠ 0, то равенство физически не корректно. Корректное выражение закона Рауля может быть получено из закона Генри и имеет вид Рi= (Хi/Хо)Рo. Не корректным является выражение (Po - P)/Po= n*/n (n и n*– моли растворителя и растворенного вещества в единице объёма раствора) [6, стр.496].
2). Абсолютная энтропия S= (R/(γ -1))ln(PVγ)+ С, где С – постоянная интегрирования [4, стр.19];
а) поскольку [V] ≠0, то не определены размерности [Vγ]= ? и [PVγ]= ?;
б) так как [PVγ] =?, то остаются не ясными физический смысл и размерность [ln(PVγ)]= ? То же относится и к выражению S= СvlnТ+ RlnV + const [6, стр. 128], поскольку [lnТ] = ? и [lnV]= ? (V– объем) (корректными должны быть выражения ln(Т/То) или ln(V/Vo)).
3). В [3, стр. 89] вывод энтропии смешения Sсмеш опирается на соотношение Больцмана Sсмеш = k lnQ (k– постоянная Больцмана), в котором величина Q, образно именуемая термодинамической вероятностью, отождествляется с математической вероятностью. В результате (на примере распределения Fe и Mg) получено выражение Sсмеш = k(NlnN - NFelnNFe – NMglnNMg). Полагая N= NFe + NMg и определяя мольную долю атомов Fe через XFe = NFe/(NFe + NMg) (также для XMg), приходим к равенству Sсмеш = nR(XFelnXFe + XMglnXMg). Поскольку [XFe] ≠0 и [XMg] ≠0, то выражение для Sсмеш не имеет физического смысла, так как физически не определены его члены lnXMg и lnXFe. Здесь просматривается и еще одна неопределенность. Произведение XFelnXFe можно представить как ln[(XFe)XFe]; это выражение физически не корректно, поскольку не ясно значение степени [(XFe)XFe]. Другими словами не ясно, что означает (2 кг)2кг и т.д.
III. Проведем некоторое обобщение. Примем, что если величина A имеет размерность, то [A] = 1. Если величина B безразмерна, то [B] = 0. В дальнейшем эти величины заменим выражениями [1] и [0] соответственно.
Основные свойства названных множеств.
- [11]x[12] = [13] (x– знак умножения);
- [01]x[02] = [0];
- [1]x[0] = [1];
- [11]x[12] = [12]x[11];
- [01]x[02] = [02]x[01];
- [1]x[0] ≠ [0]x[1];
Действительно, мы знаем произведение 2 кг яблок на 2, но мы не знаем, что означает цифру 2 умножить на 2 кг яблок.
Введем операцию деления [A1]/[A2].
- Если [11] ≠ [12], то [11]/[12] = [13];
- Если [11]=[12], то [11]/[12] = [0];
- [1]/[0] = [1];
- [0]/[1] = ?
Действительно, мы знаем, что означает деление 2 кг яблок на 2 – это деление массива яблок на две части; но мы не знаем, что означает деление цифры 2 на 2 кг яблок.
- Если [11]=[12], то [11] + [12] = [1] =[12] + [12];
- Если [11] ≠ [12], то [11] + [12] = ?.
- [1] + [0] = ? = [0] + [1].
Действительно, мы знаем, что означает сумма 2 кг яблок и 3 кг яблок, но мы не знаем, что означает сумма 2 кг яблок и 3 кг железа.
Введем операцию вычитания. Тогда:
- Если [11]=[12], то [11] - [12] = [11];
- Если [11] ≠ [12], то [11] - [12] = ?.
Действительно, мы знаем, что означит от 5 кг яблок отнять 3 кг яблок, но мы не знаем, что означит от 5 кг яблок отнять 3 кг железа.
- [1] - [0] = ? = [0] - [1].
IV.С этих позиций рассмотрим размерность некоторых физико-химических параметров. Проблема возникла в связи с анализом геохимических геотермометров, используемых для определения температуры образования минералов и имеющих вид
lnKp = -A/T + B. (2).
Здесь Кр – коэффициентом распределения элементов между минералами в результате осуществления некоторой реакции обмена, Т – абсолютная температура оК, А и В –постоянные, физический смысл которых до сих пор не определен. В основе этого выражения (2) лежат представления о химическом потенциале. Понятие о химическом потенциале является фундаментальным и лежит в основе решений многих задач в физической химии. Классическое выражение химического потенциала имеет вид μ = μо + RTlnM, где М – концентрационный параметр. Поскольку по определению [μ]= [μо]= [RT] ≠ 0, то должно быть [lnM] = 0 и [M] = 0 на основе свойств логарифмов.
В термодинамике М= aij- активность. По [1, стр. 38] «активность компонента i в фазе j отражает разницу между химическими потенциалами (μij) при данных Р, Т и составе и (μiо) в стандартном состоянии при Ро и То». Эта формулировка не является определением, а отражает только смысл предполагаемого определения; назовем его полуопределением.
Наиболее четкое понимание активности имеется в термодинамике газов [1, 3]; для идеальных газов принято, что а = Р/Ро [1, стр. 40], т.е. [а] = [Р/Ро] = 0. Для неидеальных газов принято понятие «фугитивности (летучести)» f= f(P)- некоторой функции от давления. Тогда a(f) = f(Р)/f(Ро) [1, стр. 40; 3, стр. 159]. Согласно [1, стр. 40] [f] = [P], следовательно [a(f)]= 0. Вводится также соотношение fi= ΓiPi, где Γi– коэффициент фугитивности. Так как [f] = [P], то должно быть [Γi] = 0 и Γi – безразмерная величина. Заметим, что возможные пределы изменения параметра Γi не известны, не ясна физическая сущность равенства fi= ΓiPi. Предположительно, параметр fi – это эффективное давление, отражающее количество, а Γi – долю газа, ведущего себя как идеальная субстанция. В этом случае 0≤ Γi ≤1. Тогда правильно а = ΓiРi/ΓoРо.
В термодинамике растворов ситуация не такая ясная. Для равновесия жидкость – пар [3, стр. 149] принято, что μо(ж) = μо(п) + RTlnpo. Но [po] ≠ 0; следовательно, выражение lnpo не имеет физического смысла. Далее на основании закона Рауля RTlnpi = RTlnpoi + RTlnXi, откуда следует ln(pi/poi) = lnXi, но [pi/poi]= 0, а [Xi] ≠ 0, получилось несоответствие размерностей. В целом, выражение активности зависит от «выбора единицы концентраций» [3, стр.155], что является произволом; допускаются представления: RTlnai = RTlnγxXi (или = lnγmmi или = lnγCCi, здесь mi – моляльность и Ci – молярность). Доказательства равносильности этих выражений отсутствуют. Если γ= 1, то ai = Xi (или = mi, или = Ci). Откуда [ai] ≠ 0, но тогда смысл lna становится не ясным. В этом случае понятие «активности» не соответствует таковому в теории газов.
В теории растворов нет подобных выводов. Считается, что в выражении lnM параметр М является безразмерной величиной на том основании, что концентрация раствора сравнивается с некоторой исходной концентрацией Со, принимаемой равной единице. Пример подобных рассуждений приведен в [1, 3]. При этом упускаются два обстоятельства.
1). Сравнение членов уравнения с некоторой величиной в указанном смысле возможно лишь, если этой величине определено место в исследуемом уравнении. В уравнении химического потенциала это место не определено. Это было бы сделано, если бы химический потенциал выражался уравнением μi = μоi + RTiln(Ci/Co). Но этого ни в одном выводе нет.
2). Тем не менее, видимо, по умолчанию это предполагается, поскольку существует договоренность, что Со принимается равной единице. При этом, правда, не ясно, какую размерность эта единица имеет. Таким образом величина Со = 1 является произвольной, и нет доказательств того, что различные несоответствия, возникающие при использовании химического потенциала, не вызваны этим произволом.
3). Нет доказанной связи между величиной μоi и значением Co =1. Так О.М. Полторак [3] выводит значение μоi, не связывая его не только с равенством Co =1, но и любым другим значением Со.
В термодинамике газов между Р и а существует трехступенчатая цепочка параметров: Р →Γ→ f →a. В термодинамике твердых растворов – только двухступенчатая цепочка: Х → γ →а. Для полной аналогии в последнюю необходимо ввести член Х* = γХ. Тогда цепочка примет вид Х→Х*→ γ→ а. Член Х* характеризует эффективную мольную долю компонента, играющую роль идеальной субстанции. В таком случае 0 < γ < 1. Это условие можно записать и для стандартного состояния Хо* = γоХо. Тогда выражение активности должно иметь вид а = γХ/γоХо = Γ(Х/Хо). Параметр Γ = γ/γо интерпретируется как показатель неидеальности твердого раствора. Ясно, что в таком варианте возможно неравенство Γ > 1, что не совсем понятно.
Учитывая важность понятия размерности в решении геологических задач, согласно [9] уравнение геохимического геотермометра имеет вид
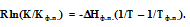
где К и Кфп- значения коэффициентов распределений двух элементов между двумя минералами при температурах соответственно Т и Тфп, dН- теплота фазового перехода (плавления минералов). Теоретическая основа этого геотермометра опирается на следующее уравнение изобары
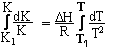
химической реакции. Поскольку уравнение геотермометра представляет собой уравнение прямой линии, то параметр Тф.п. можно заменить любой другой точкой Т2 с соответствующей ей величиной коэффициента К2.
При учёте принципа размерности уравнение химического потенциала имеет вид μ = μо + RTln(С/Со). Это выражение есть решение аналогичного определённого интеграла вида
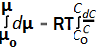
Таким образом правильная запись математического уравнения или выражение может несколько видоизменить его интерпретацию
Литература.
1. Вуд Б., Фрейзер Д. Основы термодинамики для геологов. – М.: Мир, 1981. 184 с.
2. Макаров В.П. Методические аспекты геохимической геобаротермометрии./ Материалы XIII Геол. съезда республики Коми «Геология и минеральные ресурсы Европейского Северо-востока России. Новые результаты и новые перспективы. Сыктывкар, 1999, стр. 60-63.
3. Полторак О.М. Лекции по химической термодинамике. М.: Высшая школа, 1971. 256 с.
4. Румер Ю.Б. и др. Термодинамика. Статистическая физика и кинетика. М.: Наука, 1972.
5. Чертов А.Т.Единицы физических величин.М.: Высшая школа, 1977.287с.
6. Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. М.: Наука, 1979. 551 с.
7. Макаров В.П. Некоторые свойства геохимических геотермометров./ Мат-лы XV научного семинара «Система планета Земля». М.: ЛКИ, 2007, С.142- 159.
8. Макаров В.П. О механизме выделения минералов./ Мат-лы XVI научного семинара «Система Планета Земля». М.: ТОО «Гармония строения Земли и планет», 2008. С.265 – 300.
9. Макаров В.П. Некоторые свойства геохимических геотермометров. / Мат-лы XV научного семинара «Система планета Земля». М.: ЛКИ, 2007, С.142- 159.
Источник: Макаров В.П. К теории размерности физических величин./Материалы XV научного семинара "Система планета Земля№. М.: ТОО "Гармония строения Земли и планет. 2008. С. 265 - 300.
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии