Вопросы теоретической геологии.
11. Геоспидометр - метод определения палеоскоростей перемещения древних осадков водными потоками.
В.П. Макаров
Российский государственный геологоразведочный университет, г. Москва.
В формировании осадков существенную роль играют транспортировка и отложение из водных потоков слагающих осадочные толщи компонентов, подчиняющиеся законам гидродинамики. В технике такие процессы изучаются в разделе о гидротранспорте [5]. Однако идеи [5], способствующие пониманию механизмов образования осадочных толщ, не только не нашли дорогу в литологию, но литологи не хотят знать о существовании этого важного для литологов раздела гидравлики. Негативную роль в решении проблемы сыграли и специалисты по гидравлике. Под давлением геологов (литологов) они не различают принципиально разные задачи- прямую и обратную. По своей сущности литологи занимаются решением именно обратных, а специалисты по гидравлике - прямых задач. Игнорирование существования этих задач приводит, во-первых, к тому, что специалисты по гидравлике не разрабатывают решений обратных задач, крайне нужных литологам. Во-вторых, из-за редких, по солдафонски прямолинейных внедрений решений прямых задач в литологию, предлагаемые ими решения обратных задач приобретают качественный, поверхностный, часто не корректный характер (например, [14]).
В литологии строгого анализа методов определения этих скоростей не существует. Скорости перемещения осадков, определяющие дальность переноса частиц, до сих пор (т.е. более 50 лет, начиная с работ Энгельгардта (1941 г.) [12]) определяются только качественно, путем сравнением размеров частиц на основе теоретических и экспериментальных исследований по определению скоростей отрыва (начало трогания) частицы со дна потока. Эти результаты используются при анализе движения зёрен в конкретном природном потоке, хотя скорость отрыва является минимальной скоростью перемещения частицы. Реальные скорости перемещения много больше, о чем свидетельствуют эксперименты по определению скоростей движения меченых частиц [3]. Понятно, что выводы, основанные только на классическом подходе, поверхностны и примитивны, а сама методика решения задачи отдаёт догматизмом.
В основе анализа движения частиц осадка в грубом приближении лежит представление о кинетической энергии движения частицы Е = Mv2/2 (М - ее масса, v – скорость движения). Так как М= Vρ(V- объем, ρ – плотность зерна в г/см3), то ясна роль этих непосредственно измеряемых параметров в изучении формирования аллювиальных отложений [15]. Величина ρустанавливается при минералогических исследованиях, важной и методически отработанной части изысканий [2, 7, 12– 15]. Определение V или заменяющей ее величины d(диаметр) в связи с громоздкостью заменяются измерением в зерне длины А, ширины В и толщины С (точнее наибольшей, средней и наименьшей значений размеров зерна), их значения не редко <1 мм. Громоздкость измерений и отсутствие ясности в их необходимости и методике использования этих результатов привели к отказу от проведения измерений и распространению ситового метода изучения осадков, сыгравшему, однако, весьма негативную роль в развитии литологических исследования, он стал тормозом в их развитии. В последние годы интерес к использованию ситового анализа упал, не оправдав надежд исследователей [11, 15]. Учитывая это, А.В. Сурков [15] возобновил измерения параметров А, В и С, веса минералов в россыпях и показал, что ситовой метод искажает не только весовые соотношения между фракциями, но и чистоту их выделения. В то же время наличие этих измерений позволило разработать решение актуальной в литологии задачи –определение скорости перемещения частиц на основе анализа совместного поведения зерен – минералов с разными плотностями. Для этого были использованы известные в гидродинамике уравнения перемещения зерен [5 - 7].
Одна из немногих идей гидродинамики (а фактически единственная), используемых для решения обратных задач литологии, – гипотеза осаждения минерала, использующая уравнение Стокса, например, в форме (1) [13, 14]
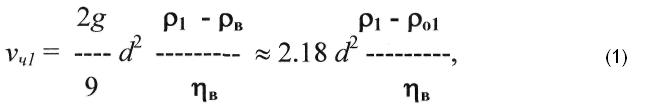
где vч1 скорость осаждения частицы диаметром dи плотностью ρ1 в воде с плотностью ρо1 и вязкостью ηв. В теории движения русловых потоков эта гипотеза играет большую роль [4]. Уравнение Стокса применялось для анализа особенностей осаждения минералов из водных потоков. Так при изучении распределений кварца Qw и магнетита Mt в предположении, что vQw = vMt, установлено, что при ρMt > ρQwобычно dMt < dQw, соответствуя качественным особенностям их распределения в реальных осадках [13, 14]. Поэтому был сделан вывод об обоснованности использования уравнения Стокса для анализа строения осадков. Ревизия этих данных не подтверждает суждение. Уравнение Стокса использовано при условии, что ρв = 1, то- есть концентрация частиц в воде мала и не влияет на плотность суспензии. Этот вывод противоречит мнению [13, 14], что формирование осадков происходят в обогащенной твердым материалом пограничной зоне, примыкающей к границе вода – осадок. Проверка уравнения Стокса на других объектах дает не совпадающие результаты. Так, в [14] описано распределение кварца Qw (ρ = 2,65г/см3), граната Gr (ρ = 3,70 г/см3) и циркона Zr (ρ = 4,70 г/см3) в осадке. Для кварца при нормальном распределении размеров зерен по оси С модальное значение dQw = 0,29 мм, для граната –dGr= 0,22 мм, для циркона –dZr- 0,16 мм. Подстановка dQwи dGrв уравнение Стокса приводит к значению ρо1 = 1,23 г/см3, говоря, что осаждение минералов происходит из суспензии. Для пары же (Qw -Zr) ρo1 = 1,85 г/см3, для пары (Gr - Zr) – 2,58 г/см3. Как видим, оценки po1разнятся. Это говорит о некорректности применяемого метода выяснения условий перемещения зерен, поэтому далее он не используется.
В основе другой гипотезы лежит представление о гидротранспорте, опирающееся на взаимоотношения потока и перемещаемых им наносов [5]. Там упоминаются напорные потоки, двигающиеся в близгоризонтальном направлении. В этом случае выделяются скорость vтр трогания (отрыва) частицы, заполонившая всю литологическую литературу, и скорость vк критическая, о которой почти не говорят. Указанные скорости выражаются следующим образом:

Здесь Vч- объём частицы, F– миделево сечение, т.е. проекция тела на плоскость, нормальную к линиям течения потока; f– коэффициент трения частицы о стенку трубы; Схт – коэффициент лобового сопротивления тела, учитывающий влияние стенок трубы на обтекание тела (частицы) потоком; Сут – коэффициент подъёмной силы; g – ускорение силы тяжести; ρч – плотность тела частицы; ρ– плотность воды.
Под скоростью трогания понимают «среднюю скорость, при которой твёрдое начинает перемещаться волочением по стенке трубы». Под критической скоростью «понимают минимальную среднюю скорость потока, при которой ещё не происходит выпадения осадка на стенку трубы.» [5, стр.146]. Ясно, что реальные скорости, определениями которых и должна заниматься литология, значительно превышают обе эти скорости.
Обе формы отличаются только значениями сопротивлений. К сожалению и здесь наблюдается застой в развитии теории гидротранспорта в изучаемом направлении. Так указанные представления почти дословно повторяются авторами [5, 6] с 1970 г. по крайней мере до 2001 г.
В работе [7] также рассмотрены вопросы о соотношениях между скоростью vч частицы в потоке и скоростью vп самого потока, и получено уравнение (4),
названное нами уравнением Гостинцева, близкое уравнению (3), где F – площадь миделева сечения; j–коэффициент

сопротивления; g – ускорение силы тяжести;Vч - объем и vч – скорость частицы. При больших скоростях vч ≈ vп [4].
Приведём некоторые замечания к уравнению (4).
1. Коэффициент φ отражает величину лобового сопротивления. Но величина сопротивления трения в формулу не входит, она учитывается только в уравнении (2). Необходимо выделение как минимум двух видов трения: трение частиц с водой потока и трение частиц между собой, поскольку во взвеси с повышенной концентрацией твердых частиц возникают постоянные взаимоотношения между частицами. Этот вид трения не изучен. Что касается первого вида трения, то оно, видимо, не велико, поскольку при попадании частицы в воду на поверхности частицы образуется монослой воды, удерживаемый на поверхности зерна молекулярными силами. Этот монослой играет роль смазки, сводящей трение между водой и частицей к трению между слоями воды. Малое значение этого трения отражается малым значением вязкости воды (0,01 пуаз). Вместе с тем и величины трения частиц между собой также не очень велики, поскольку скорость движение частиц в потоке относительно друг друга много меньше, чем скорость самого потока, а значит и взаимодействие частиц друг с другом меньше, чем взаимодействие частиц с границей канала движения. Тем не менее, далее под коэффициентом φ будем пониматьсумму сопротивлений лобового и трения.
2. Параметр Vч/F отражает линейные размеры частицы. Обобщение измерений В.А. Суркова, например, [15, 16, 19], показало, что в зернах почти всех изученных минералов (Qw, Mt, Zr и др.) песчано-алевритовой размерности в >99,0% случаев A >B >C, т.е. зерна относятся к типоморфной группе призмоидов по [17]. Поскольку F – проекция тела частицы на плоскость, то здесь возможны два крайних варианта положения тела зерна, исключая кувыркание (вращение) зерна в потоке: а) длинная ось А перпендикулярна линиям тока и б) ось А располагается вдоль этих линий тока. Тогда в первом случае F ≈ АВ (или АС)и Vч/F ≈ С (или В). Этот случай соответствует перекатыванию частицы в потоке при перемещении, способствующему истиранию частиц. Поскольку оси В и С примерно равноправны,то практически можно использовать величину С* = (С+В)/2. Во втором случае F ≈ ВС и Vч/F ≈ А.
Уравнение (4) для непосредственного изучения не годится; его необходимо преобразовать так, чтобы в качестве переменных использовались бы параметры ρ и d, непосредственно измеряемые в реальных условиях. Учитывая это, уравнение (4) преобразуется к виду
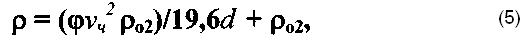
где d= V/F. Вхождение параметра vч в коэффициенты при аргументе говорит, что все зерна двигаются с одинаковыми скоростями, как и полагали Л.Б. Рухин и Н.М. Страхов [13, 14]. Принимая l = 1/d, получаем уравнение прямой ρ = βl + ρо2 (β - постоянная), а изучаемые точки должны располагаться на этой прямой. Примеры таких диаграмм, иллюстрирующие выполнение этого условия, приведены в [16, 20].
Уравнение (5) позволяет оценить скорость движения частицы в потоке по величине β, а сам метод решения задачи был назван «геоспидометр». Выявленные значения скоростей являются оценочными, позволяя, однако, проводить анализ условий перемещения осадка. Метод применён для анализа твёрдых осадков водных потоков по методике [16].
1.Изучены пески в локальной точке прибойной зоны пляжа «Зимний берег» Белого моря [15, 20]. Эта часть моря наиболее штормовая и характеризуется сильным волнением. Наибольшие скорости приливно- отливных морских течений достигают 3 м/сек. Сильные течения р. Мезень имеют скорость > 3 м/сек [10].
Результаты обработки размерных параметров зёрен приведены в табл.1 и на рис.1 и 2. По данным табл. 1 зерна имеют форму, приближенную к трехосному призмоиду. Связь формы зерен с параметрами кристалла сложная.
Таблица 1. Результаты грануло-минералогического анализа проб пляжа «Зимний берег» Белого моря
|
Минерал
|
ρ г/см3
|
Сингония
|
Параметры решетки, А
|
Средние размеры, см
|
|
ao
|
bо
|
co
|
А
|
В
|
С
|
|
Циркон
|
4,7
|
Тетрагональная
|
6,59
|
6,59
|
5,94
|
0,034 1
|
0,019 0,56
|
0,013 0,38
|
|
Гранат
|
3,7
|
Кубическая
|
11,84
|
11,84
|
11,84
|
0,053 1
|
0,039 0,74
|
0,023 0,43
|
|
Дистен
|
3,62
|
Триклинная
|
7,10
|
7,74
|
5,57
|
0,048 1
|
0,028 0,58
|
0,017 0,35
|
|
Эпидот
|
3,4
|
Моноклинная
|
8,94
|
5,61
|
10,23
|
0,052 1
|
0,034 0,66
|
0,024 0,46
|
|
Кварц
|
2,65
|
Тригональная
|
4,903
|
4,903
|
5,393
|
0,065 1
|
0,048 0,74
|
0,033 0,51
|
|
Среднее
|
|
|
|
|
|
0,050 1
|
0,035 0,667
|
0,022 0,437
|
Рис 1. Структурные спектры минералов
в россыпях пляжей Белого моря. Минералы:
1 -кварц; 2 - циркон; 3 - гранат; 4 - дистен; 5 - эпидот.
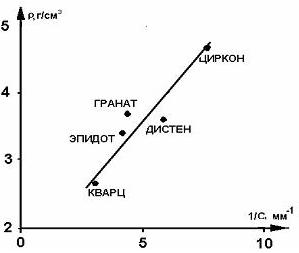
Рис.2. Диаграмма распределения в осадках Белого моря.
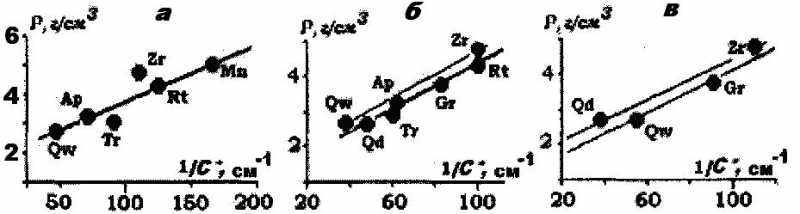
Рис.3. Распределение минералов в пробе из осадков Чудского озера. Диаграммы по группам окатанности зерен: а— неокатанные; б— полуокатанные; в— окатанные.
Распределение минералов показано на рис.2. В результате получено уравнение ρ = 0,0431/С + 1,34. Плотность суспензии, в которой перемещается частица, ρо2 = 1,34 г/см3. Кроме того β = φvч22ρо2/19,6 = φvЧ22/ 14,73= 0,0431. Опираясь на измерения параметров потоков на конкретных участках, оценим величину φ. По [4] φ = gRi/u2, где R = гидравлический радиус; для плоских потоков R= h, где h- средняя глубина и v- скорость потока; i- гидравлический уклон. Для отмелых берегов Балтийского моря [1] i = 0,016; v= 0,8 м/сек и h =2 м; поэтому φ= 0,245, а vч = 1,61 м/сек. Для φ ≈ 1 vч = 0,8 м/сек.
На рис. 1 приведен непрерывный (в смысле [16]) спектр распределения минералов в осадке, показывающий различие площадей кривых, соответствующих каждому минералу. Тогда соотношение площадей отражает соотношение минералов в осадке. По относительной распространенности (числа в скобках) минералы образуют последовательность кварц (5,2) – эпидот (3,8) – гранат (2,4) – дистен (1,8) – циркон (1), обратно пропорциональную их плотностям. Средневзвешенная плотность твердого каркаса осадка ρм = 3,24 г/см3.
Исследования показали, что поток осадков на побережье Белого моря имеет плотность 1,34 г/см3, скорость 1,61 м/с, мутность 17%. Эти параметры не соответствуют потокам осадков пониженной плотности в спокойных условиях. Подобные параметры возникают при больших скоростях течений штормовых волнений. Тогда частицы находятся в полувзвешенном состоянии, и все движение приобретает характер медленного течения грязевой массы [4].
2. Проанализирован гранулометрический состав осадков современной прибойной зоны северного побережья Чудского озера (Эстония, Кохтла-Ярвинский район, дер. Кауксу) в валовой пробе (вес = 1 кг) с глубины 0,15 м [16]. Поскольку проба единичная, то она характеризует локальные особенности осадка.
Форма зерна отлична от сферической, для всех зерен А/В>>1и С/В<< 1. Размеры не окатанных зерен меньше, чем у полуокатанных зерен, но последние всегда больше, чем у окатанных. Для оценки гидродинамических условий перемещения зерен диаграммы ρ = b/С + А (b и А- постоянные) построены по данным модальных значений главных компонент структурных спектров (рис.3) по [16]. За основу взята координата С* = (В+ С)/2. Результаты (рис.3) оказались приемлемым, поскольку практически нет расщепления диаграмм, что естественно для минералов, мигрирующих в одинаковых гидродинамических условиях и отобранных из одной пробы. Тогда для окатанных зерен получено уравнение ρ= 0,0413/С* + 1,07.
3. Исследованы диопсид(Dio), турмалин (Tur), рутил (Rut) , Zr из осадочных образований такатинской свиты (D2) на западном склоне Урала, сложенных полевошпат – кварцевыми песчаниками, часто косослоистыми, с прослоями мелкогалечных конгломератов, реже глинистых сланцев [16]. Не окатанные зерна минералов описывается уравнением ρ= 0,024/C +1,20 (показаны на рис.4).
Табл.2. Сводные параметры размеров полуокатанных зерен минералов (Таката)
|
Минерал
|
ρ г/см3
|
2/(В+C) (1/мм)
|
|
неокат
|
полуок
|
окатан
|
|
Tur
|
3,00
|
8,133
|
8,11
|
8,39
|
|
Dio
|
3,30
|
2,922
|
нет
|
нет
|
|
Rut
|
4,25
|
12,48
|
10,93
|
10,06
|
|
Zr
|
4,70
|
15,07
|
13,34
|
6,22
|
Рис.4 Диаграмма распределения полуокатанных
зёрен минералов такатинской свиты.
4. Изучены Ilm(ильменит), Qw, Rut и Zr из осадочных пород девонского (?) возраста Гвинеи (Гуаль). Распределение Qw, Rut и Zr показано на рис. 5 и описывается уравнением ρ= 0,0862/C* + 2,14.

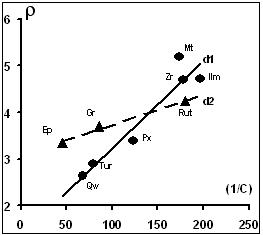
Рис.5. Распределение зерен минералов Рис.6. Распределение зерен минералов
местечка в осадках Гуаль (Гвинея). в осадках р. Угра
5. Для р.Угры (Калужская обл.) естественная скорость течения около 0,6 м/с, при половодье и паводках > 1,5 м/с. Для речных систем эти данные использованы в качестве эталона при оценке величины φ (=0,12 для vч= 1,5 м/с). Изучены минералы (Mt, Ilm, Zr, Px (авгит?), Qw, Tur) и (Ep, Gr, Rut) из донных отложений в локальной точке современного русла. Результаты отражены на рис.6. Для членов первой группы получено ρ = 0,0188/С + 1,36; второй – ρ = 0,0065/С + 3,09.
6. В локальной точке мелкого левого притока р. Угры взята донная проба с интервала 0,0 – 0, 1 м при глубине воды 15 см. Проба сложена современными русловыми отложениями, представленными песчано–гравийным, хорошо промытым материалом. Выделены группы минералов из донных отложений: 1-(Qw,Tur, авгит(?), Rut, Zrn) и 2- (Dio(?), Dis, Ep, Ilm, Mt). Для группы 1 ρ= 0,0163/С + 1,73; для группы 2 ρ= 0,01583/С + 2,77 (не четкое).
7. Распределение минералов Qw, Dis, Gr, Rut, Zr, Ilm, лейкоксена (Lx), марказита (Py(M)) в четвертичной россыпи Тарского месторождения (Зап. Сибирь) показано на рис.7. и описывается уравнением ρ = 0,0124/С + 2,10.
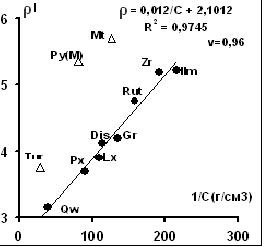
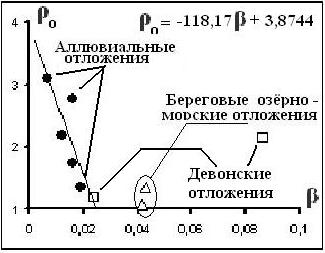
Рис.7. Распределение зёрен Рис.8. Компенсационная
минераловв россыпи Тарская. диаграмма
Вероятные скорости vч движения частиц в потоках представлены в табл.3. Эти данные выявляют сравнительно небольшие пределы колебаний скоростей перемещения зёрен. Среднее значение скорости равно 1,16 м/с; это значение можно брать в качестве эталона при оценке скорости перемещения в водных потоках зёрен песчано-алевритовой размерности.
Поскольку все уравнения, описывающие связь параметров зёрен, являются линейными уравнениями в координатах ((1/С*), ρ), то к ним применимы представления о компенсации, описанные нами при решении задач изотопии и петрологии [9]. Компенсационная диаграмма приведена на рис. 8. Визуально на рис. 8 чётко выделяются генетически различные образования: современные береговые озёрно–морские и аллювиальные отложения. Кроме того, отмечаются девонские отложения, природа которых не совсем четко проявлена. По полученным данным выборка из отложений такатинской свиты (Урал) тяготеет к аллювиальным отложениям. Пробы выборок из аллювиальных отложений попадают на прямую, описываемую компенсационым уравнением ρо = -118,17β +3,87. По
Таблица 3. Результаты определения параметров течений разных объектов.
|
Регионы
|
β
|
ρo (г/см3)
|
vч(м/сек)
|
j
|
|
Побережье Белого
моря (Россия)
|
0,0431
|
1,34
|
1,59
|
≈0,25
|
|
Чудское озеро (СССР)
|
0,0413
|
1,07
|
1,74
|
»0,25
|
|
Древний бассейн (Башкирия, Таката)0,024
|
|
1,2
|
1,25
|
|
Древний бассейн
(Гвинея, Гуаль)
|
0,0862
|
2,14
|
1,78
|
|
р. Угра. Россия,
Калужская обл.
|
0,0188
|
1,36;эталон
|
1,50
|
»0,12
|
|
0,0065
|
3,09
|
0,59
|
|
Локальный приток
р.Угры.
|
0,0163
|
1,73
|
1,24
|
|
0,01583
|
2,77
|
0,97
|
|
Тарская россыпь. Зап. Сибирь. Россия.
|
0,0124
|
2,17
|
0,97
|
По определению [9] если пучок прямых вида ρ = βi(1/С*) + ρоi сходится в некоторой точке с кооринатами ((1/С*)о, (rоi)о), то эти координаты являются параметрами компенсационного уравнения ρоi= -(1/С*)оβ +(ρоi)о, где β и ρ оi– переменные величины. Таким образом, из эмпирических данных по аллювию имеем (ρ оi)о = 3,87, а Со* = 0,0085 мм ((1/С*)о = 118,17). Однако физический смысл этих параметров, к сожалению, не ясен.
По параметрам ρо и β рассчитаны значения скоростей v движения зёрен в потоках. На рис. 9 приведена диаграмма связи между ρо и v, построенная по данным табл. 3.
Рис.9. Диаграмма зависимости
параметров ρо и v
Подавляющее большинство объектов четвертичного и современного возрастов попадают на прямую v = -0,5163ρо + 2,2249 (R2= 0,9344). От неё отскакивают только точки древних девонских бассейнов – Гуаль и Таката. Основная закономерность: наличие обратной зависимости между изучаемыми параметрами, т.е. чем плотнее взвесь, тем меньше скорость её перемещения. Это соответствует интуитивной точке зрения, что при прочих равных условиях, чем больше масса объекта, тем медленнее объект движется.
К прочим равным условиям относятся:
1) равенство кинетических энергий движения частиц. Полагая для двух взвесей с плотностями ρо1и ρо2 равенство их объёмов, получаем ρо1v12 = ρо2 v22, согласно чему и выявляется указанная зависимость. Однако относительно скоростей это равенство является квадратичным, не соответствуя полученным результатам (линейная зависимость между параметрами).
2) Равенство количества движения, т.е. импульсов J перемещения зёрен. Возможность использования J выявляется следующим образом. Согласно [19] совместное присутствие НО- , ПО- и ОК- зёрен объясняется тем, что неокатанность зёрен увеличивает площать поверхности зерна и сопротивления лобовое и трения, создавая дополнительное воздействие потока на зерно. Это выводится из уравнения (4). По указанным выше обстоятельствам уравнение (4) перепишем в виде Сφ= (ρo/(ρ - ρo)(vч2/2g). Применив последнее для двух зёрен и сократив равные элементы, получаем С1φ1 = C2φ2= Сφ= const. Установим физический смысл Сφ. Одно из значений J- коэффициент сопротивления, который определяется уравнением F = φv, где v- скорость движения зерна, F- сила, действущая на зерно. Тогда в системе СИ размерность [φ] = кг/сек. Поскольку [C] = м, то [Сφ] = кгм/сек = [mv], это есть размерность импульса J.
Поскольку J = mv, тогда при условиях, описанных в п.1, ρо1v1=ρо2 v2. Это соответствует имеющимся результатам и говорит об импульсной (пульсационной) природе движения взвешенной массы в потоке.
Пульсационный характер перемещения материала позволяет говорить о периодичности протекания процесса; в качественном плане эта периодичность описывается гиперболическим уравнением (d2M/dt2) = v2(d2M/dx2). Вывод этого уравнения приведён в [20]. Здесь М- масса переносимого вещества. Вывод опирается на аксиомы:
1.Перемещение осадочного материала осуществляется как в декартовом пространстве, так и во времени. Это позволяет записать выражение М = f(x,t), где х - координата, вдоль которой происходит это перемещение; t- время.
2. Осадочный материал поступает в бассейн вследствие разрушения некоторого исходного материнского геологического тела, заполненного рыхлым материалом, причём количество выносимого материала пропорционально количеству материала в геологическом теле. Это позволяет записать исходные уравнения в виде dM/dx = - axM; dM/dt = - atM.
В случае стационарности процесса переноса, т.е. при dM/dt= 0, получаем классическое решение в виде экспоненциальной зависимости [4]. Второе уравнение аналогично уравнению радиоактивного распада. Дальнейшее преобразование исходных уравнений приводит к упомянутому гиперболическому уравнению. Это уравнение часто называют уравнением струны, отражая колебательный (периодический) характер движения струнных точек.
Оценено положение осей зёрен относительно направления движения потока. Анализ показал, что чаще всего аргументом является величина (1/С*)(С* = (В+ С)/2), говоря о том, что зерно ориентировано поперек течения. Это допустимо при перемещении зерна перекатыванием. Этот вывод соответствует многим известным экспериментальным и натурным наблюдениям, в тоже время он не соответствует утверждениям, что главным механизмом перемещения зерна является скачок [4].
Таким образом, проведенные исследования с помощью нового метода определения палеоскоростей движения потоков позволили выявить некоторые особенности перемещения минералов водными потоками.
В работе [16] описана методика работы со спектрами, которая позволяет оценивать скорость и мутность потока- суспензии. Сравнение спектров для двух объектов позволяет оценить относительную интенсивность движения этих потоков. Для этого рассмотрим кинетические энергии этих потоков E1 = Σ(m1v1 )/2 и Е2 = Σ(m2v2)/2. Для всех частиц суспензии скорости равны, поэтому можно записать Е1 = (v12)Σm1/2 и Е2 = (v22)Σm2/2. За основу анализа взят кварц, как главный транспортирующий агент в потоках на Беломорье и в Чудском озере, поэтому оценивается парциальная интенсивность движения потоков. Скорости движения частиц известны и, полагая М1= Σm1, М2 = Σm2, получаем E1 /Е2 = KM1/M2, где К = (v12)/(v22). В случае использования представлений об импульсном механизме движений К = (v1)/(v2). Для упрощения положим К = 1. Так как М = Vρ, то Ег/Е2 = V1/V2 ≈ S1/S2, где S = Р·Δl - площадь графика между линией спектра и осью абсцисс, Р - средняя величина встречаемости зерен заданного размера (средняя частота встреч, %), Δl= lmax - lmin- размах основания структуры; lmin и 1тах- минимальные и максимальные размеры зерен. Для примера на рис.10 приведены структурные непрерывные спектры по осям С в осадках Белого моря и Чудского озера по материалам [15, 16]. Для осадков Белого моря S1= 22,8 условных единиц (у.е.), для осадков Чудского озера - 0,91 у.е.; К= (v12 )/(v22 ) ≈1. Тогда E1/Е2 = 22,8/0,91 = 25. Это означает, что интенсивность перемещения суспензии кварца в Белом море примерно в 25 раз выше, чем в потоках Чудского озера.
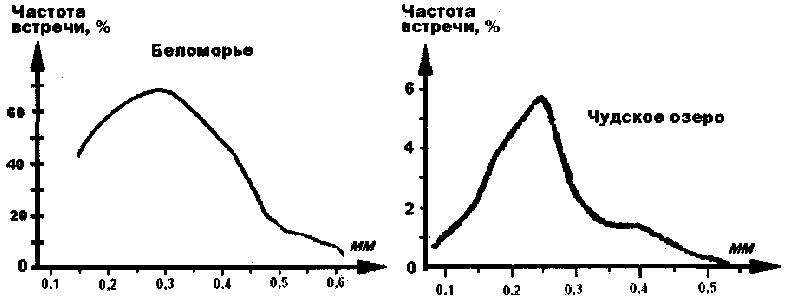
Рис.10. Структурные непрерывные спектры по оси С в осадках
Белого моря и Чудского озера.
Дополнение 2.
В уравнении (5) большую роль играет величина объема V частицы. В работе [19] показано, что зёрна имеют призмоидную форму. Её объем определяется из равенства V= ABC, однако это равенство отражает идеализированную форму; практически эта форма отличается от таковой. Для окатанных зёрен форма зерна приближается к эллипсоидной форме, что вызывает необходимость применения поправочного коэффициента 2π/9 ≈ 0,70. Для неокатанных зёрен это различие ещё больше. Например, объём треугольной пирамиды с высотой С, длиной стороны треугольника основания А и высотой треугольника основания, опущенной на сторону А, -В, равен (1/6)АВС, поправочный коэффициент равен ≈0,33; то- есть, величина поправочного коэффициента ещё меньше. Этот материал позволяет по-новому оценить понятие «степень окатанности» зёрен, установить его настоящее место в литологии и выявляет необходимость учёта его при оценке скорости движения частиц в виде некоторых поправочных коэффициентов.
Литература.
1.Айбулатов Н.А., Долотов Ю.С., Орлова Г.А.и др. Некоторые черты динамики отмелого песчаного берега. / Исследование гидродинамических и морфодинамических процессов береговой зоны моря. М.: Наука, 1966. С. 38-103.
2. Батурин В.П.Петрографический анализ геологического прошлого по терригенным компонентам. М.: Издательство АН СССР, 1947. 335 с.
3. Болдырев В.Л., Зенкович В.П. и др. Применение люминесцентных меченых песков для изучения перемещения морских и речных наносов. /Процессы развития и методы исследования прибрежной зоны моря. М.: Наука, 1972. С. 4-26.
4. Великанов М.А.Динамика русловых потоков. Т. П. М.: Гостехиздат,
5. Гейер В.Г. и др. Гидравлика и гидропривод. М.: Недра, 1991. 331 с.
6. Гудилин Н.С. и др. Гидравлика и гидропривод. М.: издание МГУ,2001.519 с.
7. Гостинцев К.К. Метод и значение гидродинамической классификации песчано- алевритовых пород при поисках литологических ловушек нефти и газа.// Методика прогнозирования литологических и стратиграфических залежей нефти и газа. Л.: Издательство ВНИГРИ, 1981. С. 51-62.
8.Жуковец A.M.Моделирование процесса перемещения морских песчаных наносов.// Исследование гидродинамических и морфодинамических процессов береговой зоны моря. М.: Наука, 1966. С. 104- 111.
9.Макаров В.П.«Явление компенсации»- новый вид связи между геологическими объектами. /Мат- лы I международной научно- практической конференции «Становление современной науки – 2006». Т.10. Днепропетровск: «Наука и образование», 2006. С. 85- 115.1955. 323 с.
10. Медведев B.C. Схема литодинамики и баланс наносов северной части Белого моря. /Процессы развития и методы исследования прибрежной зоны моря. М.: Наука, 1972. С. 27- 53.
11.Романовский С.И. Физическая седиментология. Л.: Наука, 1988. 239 с.
12.Рухин Л.Б. Гранулометрический метод изучения песков.Л.:Изд-во ЛГУ,1947.213с.
13.Рухин Л.Б. Основы литологии. Л.: Недра, 1969. 491 с.
14.Страхов Н.М. Осадконакопление в современных водоемах. М: Наука, 1993.394 с.
15.Сурков А.В. Методика грануло-минералогического анализа при изучении обломочный пород. // Изв. вузов. Сер. Геология и разведка, 1993. 3. С. 36-43.
16.Сурков А.В., Фортунатова Н.К., Макаров В.П. Об условиях образования
современных осадков Чудского озера по гранулометрическим данным.// Изв. вузов.
Сер. Геология и разведка, 2005. 5. С. 60 - 65.
17. Макаров В.П. Вопросы математической геологии. 4. К определению понятия «обломочные породы»./Мат-лы междунар. научно- практич. конф-ции «Научные исследования и их практическое применение. Современное состояние и пути
развития ‘2007». Т.16. Одесса:«Черноморье, 2007. С. 20- 27.
18. Макаров В.П. Вопросы математической геологии. 7. Элементы теории структур./ Материалы междунар. научно- практич. конф-ции «Современные проблемы и пути их решения в науке, транспорте, производстве и образовании ‘2007». Т.19. Одесса:«Черноморье», 2007. С. 27- 39.
19. Макаров В.П., Сурков А.В. Вопросы теоретической геологии. 9. Некоторые морфологические свойства зёрен в рыхлих осадочных породах. /Материалы междунар. научно- практич. конф-ции «Современные направления теоретических и прикладных исследований-‘2008. Т. 23. Одесса: «Черноморье», 2008, С.32- 44.
20. Макаров В.П. Вопросы теоретической геологии. 10. К проблеме механизма перемещения и осаждения твёрдого вещества из водных потоков./Мат-лы междун. научно- практич. конф-ции «Современные направления теоретических и прикладных исследований.-‘2008». Одесса: Черноморье, 2008. Т.23. С. 44- 56.
Примечание: источник- Макаров В.П. Вопросы теоретической геологии.
11. Геоспидометр - метод определения палеоскоростей перемещения древних осадков водными потоками.// Международная научно-практическая конференция «Перспективные инновации в науке, образовании, производстве и транспорте’2008».// Одесса: Черноморье, 2008. Т.15. С.36-49.
Комментарии
You may like my work in Sand Texture Sedimentology
Dear Mr. Surkov,
From your papers I see that you may like my theoretical and practical work in Sand Texture Sedimentology. You are welcome on my web pages: http://www.grano.de (in January: http://www.granometry.com ).
Let me know your opinion to jb@grano.de
Best wishes & do svidania,
Jiri